competencias genéricas y específicas - YouTube
La interpolación lineal es una caso particular de la
interpolación general de Newton.
Con el polinomio de interpolación
de Newton se logra aproximar un valor de la función f(x) en un valor
desconocido de x. El caso particular, para que una interpolación sea lineal es
en el que se utiliza un polinomio de interpolación de grado 1, que se ajusta a
los valores en los puntos X0 y X1. Se denota de la siguiente manera:
Ejemplo matematico:
empleando la formula anterior
procedemos a calcular el valor que tendría el sensor en la medicion
correspondiente a 3.5
f(3.5)= 46+
[(44.7-46)/(4-3)]*(3.5-3)=45.35
de igual forma se procedió a
hacer los cálculos para cada valor. Los resultados fueron los siguientes:
¿Qué es la
interpolación de Lagrange?
La interpolación de Lagrange es
un método numérico de aproximación de funciones, el cual hace uso de un
polinomio que pasa por ciertos puntos conocidos de la función que se pretende
aproximar.
Si la función a aproximar es
suave, aún fuera de los valores dados o conocidos, el polinomio toma valores
cercanos a los de la función de interés, sobre todo si dichos valores están
comprendidos entre los puntos dados. Por eso el polinomio se considera una
buena aproximación a la función.
Figura 1.- Fórmula para construir
los polinomios de Lagrange. Fuente: F. Zapata.
Interpolacion de Lagrange. Ejemplo Resuelto - YouTube
Ahora bien, supóngase que se
desea aproximar una función f(x) de la que solo se conocen sus
valores en algunos xi, con i desde 0 hasta n-1.
Es decir, se conocen n puntos (xi, yi) con yi =
f(xi), donde el índice i va desde 0 hasta n-1.
En el método de interpolación de
Lagrange, el polinomio que aproxima a la función f(x) es un
polinomio P(x) de grado n-1, construido mediante
la combinación lineal de n polinomios Li(x) de
grado n-1. Estos son los polinomios de Lagrange, que se
expresan de la siguiente manera:
Los valores de yi representan
las ordenadas correspondientes a las abscisas xi donde
la función f(x) es conocida, es decir: yi =
f(xi).
Interpolación segmentaria o splines
En el subcampo matemático del
análisis numérico, un spline es una curva diferenciable definida en porciones
mediante polinomios.
En los problemas de
interpolación, se utiliza a menudo la interpolación mediante splines porque da
lugar a resultados similares requiriendo solamente el uso de polinomios de bajo
grado, evitando así las oscilaciones, indeseables en la mayoría de las
aplicaciones, encontradas al interpolar mediante polinomios de grado elevado.
Para el ajuste de curvas, los
splines se utilizan para aproximar formas complicadas. La simplicidad de la
representación y la facilidad de cómputo de los splines los hacen populares
para la representación de curvas en informática, particularmente en el terreno
de los gráficos por ordenador.
Definición: El término "spline"
hace referencia a una amplia clase de funciones que son utilizadas en
aplicaciones que requieren la interpolación de datos, o un suavizado de curvas.
Los splines son utilizados para trabajar tanto en una como en varias
dimensiones.
Las funciones para la
interpolación por splines normalmente se determinan como minimizadores de la
aspereza sometidas a una serie de restricciones.
regresión y correlación
Para usar regresión lineal o correlación cuando se quiere
saber si una variable de medición está asociada con otra variable de medición;
desea medir la fuerza de la asociación (r2�2);
o si desea una ecuación que describa la relación y pueda usarse para predecir
valores desconocidos.
¿Qué es el método
de mínimos cuadrados?
Método de Mínimos cuadrados - YouTube
El método de mínimos cuadrados es una de
las aplicaciones más importantes en la aproximación de funciones. La idea es
encontrar una curva tal que, dado un conjunto de pares ordenados, dicha función
se aproxime mejor a los datos. La función puede ser una recta, una curva
cuadrática, una cúbica, etc.
La idea del método consiste en minimizar la suma de cuadrados de las diferencias en las ordenadas (componente Y), entre los puntos generados por la función elegida y los puntos pertenecientes al conjunto de datos.
PROBLEMAS DE
APLICACIÓN
En los problemas de caída libre consideramos que cuando un
objeto sigue un movimiento ascendente, es decir, se mueve hacia arriba la velocidad es positiva, mientras
que la aceleración será negativa ya
que el objeto se va frenando, en caso contrario, cuando el objeto sigue un
movimiento descendente la
velocidad será negativa al igual que la aceleración.
ejemplos de
problemas de aplicación.
El proceso de solución de los problemas, ejemplifican los
procedimientos algebraicos para transformar la integral a una integral
inmediata y obtener la solución general, así mismo, la aplicación de las
condiciones iniciales para determinar la solución particular.
PROBLEMA 1
El Martín pescador viaja verticalmente a una velocidad
inicial de 100 kmh100 ��ℎ,
desde una altura de 10 metros para pescar al pez rodio que viaja gran velocidad
¿Cuál es la velocidad alcanzada por el Martín pescador al hacer contacto con el
agua?, ¿en qué instante choca con el agua? Considera que después del tiempo
cero, el movimiento del Martín pescador es en caída libre.
Resolución problema 1
Datos:
vi=−27.7 ms��=−27.7 �� (conversión de 100 kmh = 27.7 ms100 ��ℎ = 27.7 ��)
s0=10 m�0=10 �
g(t)=−9.8ms2�(�)=−9.8��2
v(t)=∫−9.8dt=−9.8t+C�(�)=∫−9.8��=−9.8�+�, solución general.
v(0)=−9.8(0)+C=−27.77�(0)=−9.8(0)+�=−27.77, por lo que C=−27.77�=−27.77 y sustituyéndola
en la función velocidad resulta la solución particular:
v(t)=−9.8t−27.77�(�)=−9.8�−27.77
Para obtener la velocidad del Martin Pesador cuando hace
contacto con el agua debemos determinar la función posición y con ésta el
tiempo cuando hace contacto con el agua.
s(t)=∫(−9.8t−27.77)dt=−4.9t2−27.7t+C�(�)=∫(−9.8�−27.77)��=−4.9�2−27.7�+�,
solución general.
s(0)=−4.9(0)2+27.77(0)+C=10�(0)=−4.9(0)2+27.77(0)+�=10, por lo que C=10�=10 y al sustituirla en la
función posición resulta la solución particular.
s(t)=−4.9t2−27.7t+10�(�)=−4.9�2−27.7�+10
Para obtener el tiempo cuando Martín Pescador hace contacto
con el agua debemos resolver la ecuación s(t)=0�(�)=0,
es decir,
s(t)=−4.9t2−27.77t+10=0�(�)=−4.9�2−27.77�+10=0
t=−b±b2−4ac√2a=27.77±(−27.77)2−4(−4.9)(10)√2(−4.9)=27.77±967.1229√−9.8=27.77±31.09−9.8�=−�±�2−4��2�=27.77±(−27.77)2−4(−4.9)(10)2(−4.9)=27.77±967.1229−9.8=27.77±31.09−9.8
t1=−6�1=−6, t2=0.33�2=0.33 se toma el tiempo
positivo ya que el negativo no tiene sentido en el contexto del problema.
Por lo que la velocidad de Martín Pescador al hacer contacto
en el agua es:
v(0.33)=−9.8(0.33)−27.77=−31.004 ms



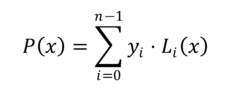



No hay comentarios:
Publicar un comentario